Reproducible Random Number Generation using Unpredictable Random Numbers

The use of random numbers in simulation is widespread, and is crucial in a large number of applications. In simulation, it is equally important that applications using random numbers are reproducible. The requirement of reproducibility is important for many reasons:

1. Code development and debugging would be nearly impossible without reproducible random numbers
2. Many simulation applications require absolute reproducibility in certification situations, such as those mandated by the Nuclear Regulator Commission
3. Publication in many journals now has a code reproducible mandate, such as the ACM Transactions on Mathematical Software.

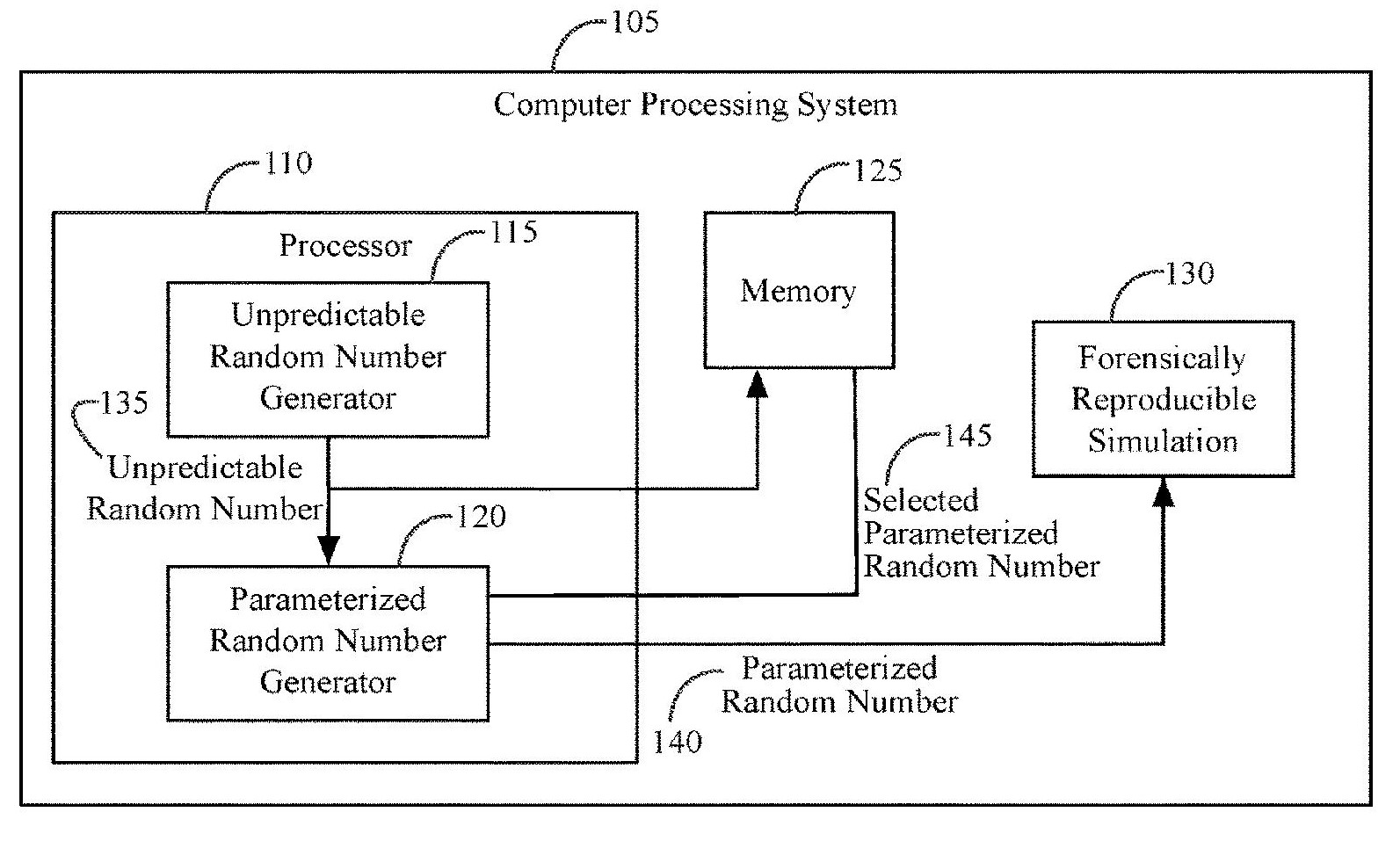
This has led to many new, and very capable random numbers designed primarily for cryptographic use, and hence are unpredictable, to be deemed inadequate for simulation purposes. One such generator, the Intel digital random number generator (DRNG) is of particular note, and served as Dr. Mascagni’s inspiration.

In the Scalable Parallel Random Number Generators (SPRNG) library that Dr. Mascagni developed, one has the capability to produce independent full-period random number streams based on parameterization. The parameter can be thought of as a very long integer, and SPRNG currently assigns parameters to steams. One can use an unpredictable RNG to produce the parameters in SPRNG, and by augmenting the SPRNG RNG data structure, this can be done in a reproducible way. The reproducibility will be of the so-called forensic type, and reproducing the results will require the use and design of extra software to collect the parameters used in a computation, and to stage a new computation with the same parameters.

Advantages:

• All current Intel and AMD processors have an interface to the RdRAND function, which produces the unpredictable random values. Thus, this would provide a reproducible generator for a wide variety of machines, and would permit parallel and distributed computing without the need for message passing, as the Native RdRAND function can be used independently.